Day 15. 今天不寫程式改來學知識 #3：Local坐標系之正形與仿射轉換

第 12 屆 iThome 鐵人賽

DAY 15

Modern Web

WebGIS入門學習 - 以Openlayers實作系列第 15 篇

12th鐵人賽 conformal affine geocoordinate webgis

JYHsu

2020-09-25 04:04:30

4960 瀏覽

前言

寫到Day15只有一個感想：恩...我的文章怎麼寫得越來越長
其實這次鐵人賽的每一篇都差不多是我一個晚上下班後寫的量，原本覺得還好，但文章打起來怎麼落落長，而且寫文章的時間還比寫程式的時間多太多了囧

但我們今天還是要稍微提到一下坐標轉換的部分，相信大家已經開始對坐標系統感到厭煩了，已經是最後一篇了最後！！
在 Day 13 時我們提到 TWD67 無法靠橢球參數轉換到WGS84或TWD97，因此要使用控制點來進行兩者之間的轉換，也就是今天主要要說明的內容。

今天的大綱

平差解算求得最佳解
四參數轉換 (二維正形轉換)
六參數轉換 (二維仿射轉換)

1. 平差解算求得最佳解

採用間接觀測平差進行線性方程式求解
一組坐標可列兩條觀測方程式，假設有m條方程式、n個未知數，且觀測量之間獨立，可將公式列為：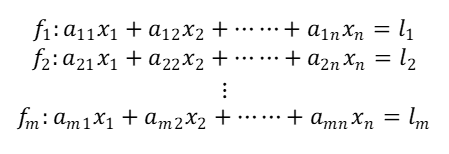

由於方程式數量m遠大於未知數數量n，以這種情形會無法有唯一解產生，而要如何得到最佳解呢？
我們給予每條觀測量一個改正數v，當改正數的平方和為最小時，即可求得最佳解。

整理成矩陣形式則為：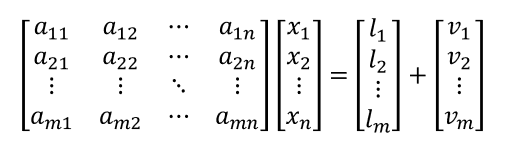

又可寫成： $AX=L+V$

在這邊就不推導了，不然會太理論大家都看不下去，而且平差就算給整個學期的課也都學不完的 ~
直接講結論，用以下公式求得未知數矩陣 X 的最佳解：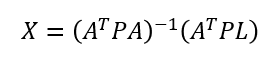

( P 為觀測方程式的權矩陣，大小為mxm的對角矩陣，若權重相同則使用單位矩陣)

因此，只要把觀測方程式整理成上述那種矩陣的形式，即可使用這個式子去求得轉換參數，求出轉換參數後，即可用這組參數代回去轉其他的坐標，達到批次坐標轉換的目的，接下來我們來看4參數和6參數的公式。

2. 四參數轉換 (二維正形轉換)

4個參數：包含一個比例尺因子S、一個旋轉量⁡⁡theta及兩個平移量∆x、∆y。
其物理意義為轉換後原為正方形之特徵物仍保持正方形狀，一般用於兩平面直角坐標系統之坐標轉換。
一組坐標可列兩條觀測方程式，4個未知數至少需要4條方程式才能求解，因此至少要2組控制點才可求得唯一解。

由於原始公式為非線性，以a、b、Tx、Ty這四個參數代之，進行線性求解
注意！！！最後求解出來的參數非上述所列的4個參數的意義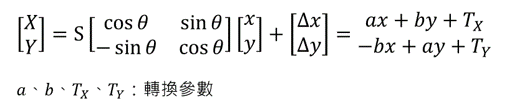

using MathNet.Numerics.LinearAlgebra;
using Newtonsoft.Json;
using System;
using System.Collections.Generic;
using System.Web.Script.Serialization;
using System.Web.Script.Services;
using System.Web.Services;

public class POINT
{
    public double x;
    public double y;
}

public class ConformalOutput
{
    public string equ_X;
    public string equ_Y;
    public double a;
    public double b;
    public double Tx;
    public double Ty;
    public double Sigma0;
    public List<POINT> Converted;
}

/// <summary>
/// TransService 的摘要描述
/// </summary>
[WebService(Namespace = "http://tempuri.org/")]
[WebServiceBinding(ConformsTo = WsiProfiles.BasicProfile1_1)]
// 若要允許使用 ASP.NET AJAX 從指令碼呼叫此 Web 服務，請取消註解下列一行。
[System.Web.Script.Services.ScriptService]
public class TransService : System.Web.Services.WebService
{
    [WebMethod(EnableSession = true)]
    [ScriptMethod(ResponseFormat = ResponseFormat.Json)]
    public string ConformalTrans(string ori_point, string control_point, string unconvert_point)
    {
        List<POINT> OriPointList = JsonConvert.DeserializeObject<List<POINT>>(ori_point);
        List<POINT> ControlPointList = JsonConvert.DeserializeObject<List<POINT>>(control_point);
        List<POINT> UnconvertPointList = JsonConvert.DeserializeObject<List<POINT>>(unconvert_point);
        if(OriPointList.Count != ControlPointList.Count || ControlPointList.Count < 2)
        {
            Context.Response.Status = "500 Invalid point number";
            Context.Response.StatusCode = 500;
            Context.ApplicationInstance.CompleteRequest();
            return null;
        }
        else
        {
            var M = Matrix<double>.Build;
            var A = M.Dense(OriPointList.Count * 2, 4);
            var L = M.Dense(ControlPointList.Count * 2, 1);
            var P = M.DenseDiagonal(OriPointList.Count * 2, OriPointList.Count * 2, 1);
            for (int i = 0; i < OriPointList.Count; i++)
            {
                A[i * 2, 0] = OriPointList[i].x;
                A[i * 2, 1] = OriPointList[i].y;
                A[i * 2, 2] = 1;
                A[i * 2 + 1, 0] = OriPointList[i].y;
                A[i * 2 + 1, 1] = -OriPointList[i].x;
                A[i * 2 + 1, 3] = 1;
                L[i * 2, 0] = ControlPointList[i].x;
                L[i * 2 + 1, 0] = ControlPointList[i].y;
            }
            var dX = (A.Transpose() * P * A).Inverse() * (A.Transpose() * P * L);
            var V = A * dX - L;
            var Sigma0 = Math.Sqrt((V.Transpose() * P * V)[0, 0] / (OriPointList.Count * 2 - 4));
            var output = new ConformalOutput()
            {
                equ_X = "X = a*x + b*y + Tx",
                equ_Y = "Y = -b*x + a*y + Ty",
                a = dX[0, 0],
                b = dX[1, 0],
                Tx = dX[2, 0],
                Ty = dX[3, 0],
                Sigma0 = Sigma0,
                Converted = new List<POINT>()
            };
            if (UnconvertPointList != null)
            {
                List<POINT> arrList = new List<POINT>();
                for (int j = 0; j < UnconvertPointList.Count; j++)
                {
                    arrList.Add(new POINT()
                    {
                        x = output.a * UnconvertPointList[j].x + output.b * UnconvertPointList[j].y + output.Tx,
                        y = output.a * UnconvertPointList[j].y - output.b * UnconvertPointList[j].x + output.Ty
                    });
                }
                output.Converted = arrList;
            }
            return new JavaScriptSerializer().Serialize(output);
        }
    }
}

3. 六參數轉換 (二維仿射轉換)

6個參數：兩坐標系間包含二個比例尺因子Sx、Sy、一個變形因子（坐標系兩軸間之非正交）epsilon、一個旋轉量theta及兩個平移量∆x、∆y。
一組坐標可列兩條觀測方程式，6個未知數至少需要6條方程式才能求解，換句話說：至少要三個共同點來求解，基本上大多數的坐標轉換均能以 a1, a2, b1, b2, Tx, Ty 此6個參數為之。

public class AffineOutput
{
    public string equ_X;
    public string equ_Y;
    public double a1;
    public double a2;
    public double b1;
    public double b2;
    public double Tx;
    public double Ty;
    public double Sigma0;
    public List<POINT> Converted;
}

[WebMethod(EnableSession = true)]
[ScriptMethod(ResponseFormat = ResponseFormat.Json)]
public string AffineTrans(string ori_point, string control_point, string unconvert_point) {
    List < POINT > OriPointList = JsonConvert.DeserializeObject < List < POINT >> (ori_point);
    List < POINT > ControlPointList = JsonConvert.DeserializeObject < List < POINT >> (control_point);
    List < POINT > UnconvertPointList = JsonConvert.DeserializeObject < List < POINT >> (unconvert_point);
    if (OriPointList.Count != ControlPointList.Count || ControlPointList.Count < 2) {
        Context.Response.Status = "500 Invalid point number";
        Context.Response.StatusCode = 500;
        Context.ApplicationInstance.CompleteRequest();
        return null;
    } else {
        var M = Matrix < double > .Build;
        var A = M.Dense(OriPointList.Count * 2, 6);
        var L = M.Dense(ControlPointList.Count * 2, 1);
        var P = M.DenseDiagonal(OriPointList.Count * 2, OriPointList.Count * 2, 1);
        for (int i = 0; i < OriPointList.Count; i++) {
            A[i * 2, 0] = 1;
            A[i * 2, 1] = OriPointList[i].x;
            A[i * 2, 2] = OriPointList[i].y;
            A[i * 2 + 1, 3] = 1;
            A[i * 2 + 1, 4] = OriPointList[i].x;
            A[i * 2 + 1, 5] = OriPointList[i].y;
            L[i * 2, 0] = ControlPointList[i].x;
            L[i * 2 + 1, 0] = ControlPointList[i].y;
        }
        var dX = (A.Transpose() * P * A).Inverse() * (A.Transpose() * P * L);
        var V = A * dX - L;
        var Sigma0 = Math.Sqrt((V.Transpose() * P * V)[0, 0] / (OriPointList.Count * 2 - 6));
        var output = new AffineOutput() {
            equ_X = "X = a1*x + a2*y + Tx",
            equ_Y = "Y = b1*x + b2*y + Ty",
            a1 = dX[1, 0],
            a2 = dX[2, 0],
            Tx = dX[0, 0],
            b1 = dX[4, 0],
            b2 = dX[5, 0],
            Ty = dX[3, 0],
            Sigma0 = Sigma0,
            Converted = new List < POINT > ()
        };
        if (UnconvertPointList != null) {
            List < POINT > arrList = new List < POINT > ();
            for (int j = 0; j < UnconvertPointList.Count; j++) {
                arrList.Add(new POINT() {
                    x = output.a1 * UnconvertPointList[j].x + output.a2 * UnconvertPointList[j].y + output.Tx,
                    y = output.b1 * UnconvertPointList[j].x + output.b2 * UnconvertPointList[j].y + output.Ty
                });
            }
            output.Converted = arrList;
        }
        return new JavaScriptSerializer().Serialize(output);
    }
}

4. 測試數據

接著我們給予一組數據進行轉換參數的測試，依照WS的Input分別建立以下三個list：

OriPointList：控制點的原始坐標值
ControlPointList：控制點轉換後的坐標值
UnconvertPointList：待轉換的坐標

var OriPointList = [
	{x: 5297.08, y: -5277.02},
	{x: 5288.72, y: -257.99},
	{x: 109.53, y: -278.9},
	{x: 121.56, y: -5292.9}
]

var ControlPointList = [
	{x: 106.057, y: 105.967},
	{x: -106.056, y: 106.039},
	{x: -105.953, y: -106.041},
	{x: 105.948, y: -105.963}
]

var UnconvertPointList = [
    {x: 1010.660,y: -3025.660},
    {x: 657.820,y: -2856.550},
    {x: 1264.430,y: -738.400},
    {x: 4328.460,y: -2684.230},
    {x: 2511.780,y: -4541.090}
]

測試呼叫Conformal的轉換WS，輸入上述三個參數，回傳得到轉換參數、單位權中誤差與轉換後的點位坐標值。

$.ajax({
    type: "POST",
    url: "WS/TransService.asmx/ConformalTrans",
    data: JSON.stringify({
        ori_point: JSON.stringify(OriPointList),
        control_point: JSON.stringify(ControlPointList),
        unconvert_point: JSON.stringify(UnconvertPointList)
    }),
    dataType: "json",
    contentType: "application/json; charset=utf-8",
    success: function (d) {
        var data = $.parseJSON(d.d);
        console.log(data)
}});

以下針對回傳的數據進行解釋：

Converted：為UnconvertPointList進行坐標轉換後的點位值。
Sigma0：為求解轉換參數時，平差解算的單位權中誤差。
a, b, Tx, Ty：4個轉換參數。
equ_X, equ_Y：所採用的轉換公式。

為什麼要列出轉換公式？
前面有提到，最後求解出來的轉換參數的意義已不再是當初的平移放大旋轉的值，而只是一個線性化後的係數代碼，因此該參數與轉換公式有很密切的關係，轉換公式不同，解算出來的4個轉換參數的值亦不相同。

OutputData_Conformal = {
	Converted: [
			{x: 10.154139710099585, y: -70.45379595719831},
			{x: 3.080699810822992, y: -85.10660242178916},
			{x: -84.92989098747529, y: -59.63422218644743},
			{x: -3.6569389669741525, y: 67.55372688020557},
			{x: 73.34700574534337, y: -8.207839181362402}
	],
	Sigma0: 2.3688869100503234,
	Tx: -115.78306345448844,
	Ty: -112.12827062849865,
	a: 0.00011663685563432687,
	b: -0.04158409172216067,
	equ_X: "X = a*x + b*y + Tx",
	equ_Y: "Y = -b*x + a*y + Ty"
}

小結

今天的內容比較難，因此讀起來會比較吃力些，但我在本篇文章也沒有提到很多的理論內容。
測量平差的內容非常多，也能應用到許多地方，例如統計回歸、參數擬合也都是平差的範疇，其解算的方法大致上可分為：直接觀測平差、間接觀測平差、廣義平差、虛擬觀測平差、序列式平差、帶有條件約制的平差等，若有興趣可以找相關文章閱讀，在此就不贅述了，不然大家就真的看不下去了。

坐標的相關文章到此結束，明天開始我們要介接一些實務上會用到的API、建立功能模組進行查詢，就以即時水位站和水位警戒值開始吧！